This post is inspired by a Bluesky post by Nick Brown. A screenshot of the post is provided below:
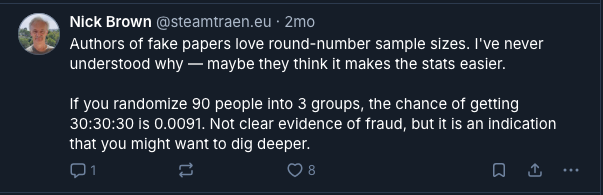
I wanted to derive this result. We need to count the following:
- The number of ways in which we can create 3 equal groups of 30, and
- The total number of ways in which we can create 3 groups from 90 test subjects
Three Equal Groups of 30 Link to heading
Starting with a subject size of 90, we can select 30 subjects from this pool in \(\binom{90}{30}\) ways.
Take these 30 subjects out of the original pool, we now have 60 subjects left. We can select 30 from this remnant pool in \(\binom{60}{30}\) ways. Taking these 30 subjects out of 60, we are left with 30 subjects, which is our third group.
The total number of ways to create 3 groups of equal size from a total subject pool of 90 is given by:
\begin{align} \binom{90}{30} \times \binom{60}{30} = \frac{90!}{(30!)^3} \tag{1} \end{align}
Create Three Groups Link to heading
We now release the restriction that the groups should have equal size. Now each subject can be allocated to any group:
- Subject 1 can be assigned to any of the three groups. This can be done in 3 ways.
- Subject 2 can be assigned to any of the three groups. This can be done in 3 ways.
- Subject 3 can be assigned to any of the three groups. This can be done in 3 ways.
… and so on. Multiplying all the ways of assigning each individual subject to one of the three groups gives us the total number of ways to create 3 groups of any size from a sample size of 90:
\begin{align} \underbrace{3 \times 3 \times \dots 3}_{90\text{ times}} = 3^{90} \tag{2} \end{align}
Chances of Getting Three Groups of Equal Size Link to heading
Putting (1) and (2) together, the chances of getting 3 groups with equal sample size is given by:
\begin{align} \frac{90!}{(30!)^3} / 3^{90} = \frac{90!}{(30!)^3 \times 3^{90}} \approx 0.0091 \end{align}
This completes the proof.
Empirical Verification Link to heading
Here’s some python code that computes the empirical probability of getting 3 groups of equal sizes from a total sample size of 90.
from random import seed, random
from collections import Counter
seed(100)
n = 1_000_000
data = range(n)
subjects = 90
def assign():
p = random()
if p <= 1/3:
return 1
elif p <= 2/3:
return 2
else:
return 3
def get_group_counts(subjects):
groups = [assign() for _ in range(subjects)]
tally = Counter(groups)
return list(tally.values())
result = [get_group_counts(subjects) for _ in data]
def get_equal_groups(result, n):
flag = [1 if ll == [30, 30, 30] else 0 for ll in result]
count = Counter(flag)[1]
return count/n
print(get_equal_groups(result, n))
## 0.009035
Which is similar to the number we got in the proof above.