In this post, I derive the expression in equation (4) of (Rossi 2014), as shown in the screenshot below.

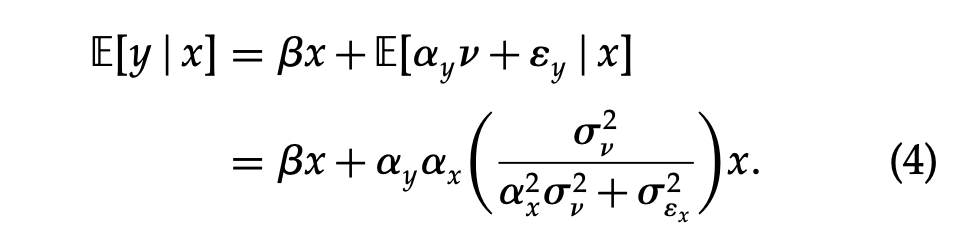
Setup Link to heading

The author provides the following system of regression equations:

\begin{align} y = & \beta x + \alpha_y v + \epsilon_y \tag{1} \\ x = & \alpha_x v + \epsilon_x \tag{2} \\ E(\epsilon_y|x, v) = & 0 \,\, \& \,\, E(\epsilon_x|x, v) = 0 \,\, \& \,\, \epsilon_y \perp\!\!\!\perp \epsilon_x \tag{3} \end{align}

In the above equations:

1. \(y, x, v, \epsilon_y, \epsilon_x\) are \(n \, \times \, 1\) vectors, where \(n\) is the number of data points. They are all assumed to be mean zero.

2. \(\epsilon_{x,i} \sim N(0, \sigma_{\epsilon_x}^2)\), \(v_i \sim N(0, \sigma_v^2)\)

3. \(E\) is the expectation operator.

4. From standard results (in the equations below, \(x'\) is the transpose of a vector \(x\); \(Var(v_i)\) denotes the variance of the random variable \(v_i\)):

   • \(Var(v_i) = E(v_i^2) - E(v_i)^2 = E(v_i^2)\), since \(E(v_i) = 0\) from 1.
   • \(Var(v) = \sigma_v^2\) from 2. Hence \(E(v_i^2) = \sigma_v^2\). Also, \(E(v'v) = E(\sum\limits_{i=1}^{n} v_i^2) = \sum\limits_{i=1}^{n} E(v_i^2) = n\sigma_v^2\)
   • \(Var(\epsilon_{x,i}) = E(\epsilon_x'\epsilon_x) - E(\epsilon_x)'E(\epsilon_x) = E(\epsilon_x'\epsilon_x)\), since \(E(\epsilon_x) = 0\) from 1.
   • \(Var(\epsilon_{x,i}) = \sigma_{\epsilon_x}^2\) from 2. Hence \(E(\epsilon_{x,i}^2) = \sigma_{\epsilon_x}^2\). Also, \(E(\epsilon_x'\epsilon_x) = E(\sum\limits_{i=1}^{n} \epsilon_{x,i}^2) = \sum\limits_{i=1}^{n} E(\epsilon_{x,i}^2) = n\sigma_{\epsilon_x}^2\)

5. The conditions from equation (3) give us the following identities:

   • \(E(x'\epsilon_y) = E(\epsilon_y' x) = 0\)
   • \(E(v'\epsilon_x) = E(\epsilon_x' v) = 0\)
   • \(E(x'v) = E(v'x) = E((\alpha_x v + \epsilon_x)'v) = \alpha_xE(v'v) + E(\epsilon_x'v) = n\alpha_x \sigma_v^2 + 0 = n\alpha_x \sigma_v^2\) (from 4b and 5b)

Omitting \(v\) Link to heading

If we regress \(y\) on \(x\) only (omitting \(v\)), we have something like this:

\begin{align} y = \beta x + \epsilon_c \end{align}

Where \(\epsilon_c\) is the “composite error term” and from (1), we have \(\epsilon_c = \alpha_y v + \epsilon_y\). The expected value of \(y\) given \(x\) (\(E(y|x)\)), is now:

\begin{align} E(y|x) = & E(\beta x | x) + E(\epsilon_c|x) \\ \implies E(y|x) = & \beta x + E(\alpha_y v + \epsilon_y|x) \end{align}

Where I use the fact that \(E(\beta x | x) = \beta E(x|x) = \beta x\) (since the expectation operator is a linear operator and \(E(x|x) = x\)). I find the value of the second term \(E(\alpha_y v + \epsilon_y|x)\).

Conditional Expectation of the Composite Error Term Link to heading

Let’s call \(z = \alpha_y v + \epsilon_y\). By construction, \(z\) is an \(n \times 1\) vector. I now regress \(z\) on \(x\), i.e. \begin{align} z = & \gamma x + \epsilon_z \\ \implies \epsilon_z = & z - \gamma x \end{align}

I want to choose \(\gamma\) in such a way that \(E(\epsilon_z'\epsilon_z)\) is minimized (ideally we want \(E(\epsilon_z'\epsilon_z) = 0\)). Said another way, we want to choose our coefficient \(\gamma\) so that the expected value of the sum of squared error terms \(\epsilon_{z,i}\) as close to \(0\) as possible (\(0\) the smallest value the sum of squared real numbers can take). When this is true, I have \(E(z|x)= E(\alpha_y v + \epsilon_y|x) = \gamma x\). Since \(\epsilon_z = z - \gamma x\), I have

\begin{align} E(\epsilon_z'\epsilon_z) = & E((z - \gamma x)'(z - \gamma x)) \\ \implies E(\epsilon_z'\epsilon_z) = & E(z'z - \gamma (x'z + z'x) + \gamma^2 x'x) \\ = & E(z'z) - \gamma E(x'z + z'x) + \gamma^2 E(x'x) \\ = & E(z'z) - 2 \gamma E(x'z) + \gamma^2 E(x'x) \tag{4} \end{align}

Where (4) follows from the fact that \(x'z\) is scalar (both are \(n \times 1\) vectors), so \(x'z = z'x\); applying the expectation operator on both sides, I have \(E(x'z) = E(z'x)\). I now take the partial derivative of (4) with respect to \(\gamma\).

\begin{align} \frac{\partial E(\epsilon_z'\epsilon_z)}{\partial \gamma} = & \frac{\partial (E(z'z)}{\partial \gamma} - \frac{\partial (2 \gamma E(x'z))}{\partial \gamma} + \frac{\partial (\gamma^2 E(x'x))}{\partial \gamma} = 0 \\ \implies & 0 - 2E(x'z) + 2 \gamma E(x'x) = 0 \\ \implies & \gamma = \frac{E(x'z)}{E(x'x)} \tag{5} \end{align}

I now want to find the values of \(E(x'z)\) and \(E(x'x)\), which is straightforward, as shown below:

\begin{align} E(x'z) = & E(x'(\alpha_y v + \epsilon_y)) \\ = & \alpha_y E(x'v) + E(x'\epsilon_y) \\ \implies E(x'z) = & n\alpha_y \alpha_x \sigma_v^2 + 0 = n\alpha_y \alpha_x \sigma_v^2 \tag{6} \end{align} Where I used the following results:

1. \(E(x'\epsilon_y) = 0\), from 5a
2. \(E(x'v) = n\alpha_x \sigma_v^2\), from 5c

\begin{align} E(x'x) = & E((\alpha_x v + \epsilon_x)'(\alpha_x v + \epsilon_x)) \\ = & E(\alpha_x^2 v'v + \alpha_x \epsilon_x'v + \alpha_x v'\epsilon_x + \epsilon_x'\epsilon_x) \\ = & \alpha_x^2 E( v'v) + 2 \alpha_x E( \epsilon_x'v ) + E(\epsilon_x'\epsilon_x) \\ \implies E(x'x) = & n\alpha_x^2 \sigma_v^2 + n\sigma_{\epsilon_x}^2 \tag{7} \end{align} Where I used the following results:

1. \(E(\epsilon_x'v) = 0\), from 5b
2. \(E(v'v) = n\sigma_v^2\), from 4b
3. \(E(\epsilon_x'\epsilon_x) = n\sigma_{\epsilon_x}^2\), from 4d

From (5), (6) and (7), I have: \begin{align} \gamma = & \frac{E(x'z)}{E(x'x)} = \frac{n\alpha_y \alpha_x \sigma_v^2}{n(\alpha_x^2 \sigma_v^2 + \sigma_{\epsilon_x}^2)} = \frac{\alpha_y \alpha_x \sigma_v^2}{\alpha_x^2 \sigma_v^2 + \sigma_{\epsilon_x}^2} \\ E(z|x) = & E(\alpha_y v + \epsilon_y | x) = \gamma x = \frac{\alpha_y \alpha_x \sigma_v^2}{\alpha_x^2 \sigma_v^2 + \sigma_{\epsilon_x}^2} x \end{align}

Which completes the proof.

Conclusion Link to heading

In this post, I derive the expression for the bias in the coefficient of \(x\), when you regress \(y\) on \(x\) without including the other independent variable \(v\). This is called the omitted variable bias, and depending on the nature of this bias, the regression could come back with spurious results, something I’ll discuss in another post.

References Link to heading