In a previous post, I called a Rust function from R and did a speed test of that function against an equivalent R function. At the end of the post, I mentioned that we could use memoization to speed up the R function. I proceed to do that here.
The speed test in the previous post might have been unfair to R, since it is well known that R is not good with recursive function calls. I now create a memoized version of the R function here:
library(rextendr)
library(ggplot2)
library(microbenchmark)
# write memoized r function
fibonacci <- function(n) {
fib <- vector('numeric', n)
for(ii in 1:(n+1)) {
# R vector indices start at 1
if(ii==1) {
fib[ii] <- 0
} else if(ii==2) {
fib[ii] <- 1
} else {
fib[ii] <- fib[ii-1] + fib[ii-2]
}
}
return(fib[n+1])
}
# run the R function
r_fn_result = fibonacci(15)
print(r_fn_result)
## [1] 610
# test run time for a larger term number
system.time(fibonacci(40))
## user system elapsed
## 0 0 0
Note that the function returns the correct value for the \(15^{th}\) term and is much faster now for generating the value of the 40th Fibonacci term (it’s even faster than the Rust function, which uses recursive function calls – see the previous post)
I now write a memoized version of the Rust function, and call it in R:
# write memoized Rust function
rust_memoized_code <- "
#[extendr]
fn fibonacci_rust(n:usize) -> i64 {
let mut fibn: Vec<i64> = vec![0;(n+1)];
for ii in 0..=n {
if ii==0 {
fibn[ii] = 0;
} else if ii==1 {
fibn[ii] = 1;
} else {
fibn[ii] = fibn[ii-1] + fibn[ii-2];
}
}
return fibn[n];
}"
# compile source code
rust_source(code = rust_memoized_code, quiet=TRUE)
# run the rust function
rustm_fn_result = fibonacci_rust(15)
print(rustm_fn_result)
## [1] 610
Which, again is the correct value for the \(15^{th}\) term. I now do a microbenchmark test:
# use microbenchmark to compare runtimes
# list of test values
values <- c(40, 50, 60)
# list to store microbenchmark results
compare <- vector('list', length(values))
for (ii in 1:length(values)) {
compare[[ii]] <- microbenchmark(fibonacci(values[ii]), fibonacci_rust(values[ii]), times = 1000)
# Change labels for plotting convenience later
# Convert expressions to character strings
expr_char <- as.character(compare[[ii]]$expr)
# Map to new labels
expr_char[expr_char == "fibonacci(values[ii])"] <- "R"
expr_char[expr_char == "fibonacci_rust(values[ii])"] <- "Rust"
# Assign the new factor with correct levels
compare[[ii]]$expr <- factor(expr_char, levels = c("R", "Rust"))
}
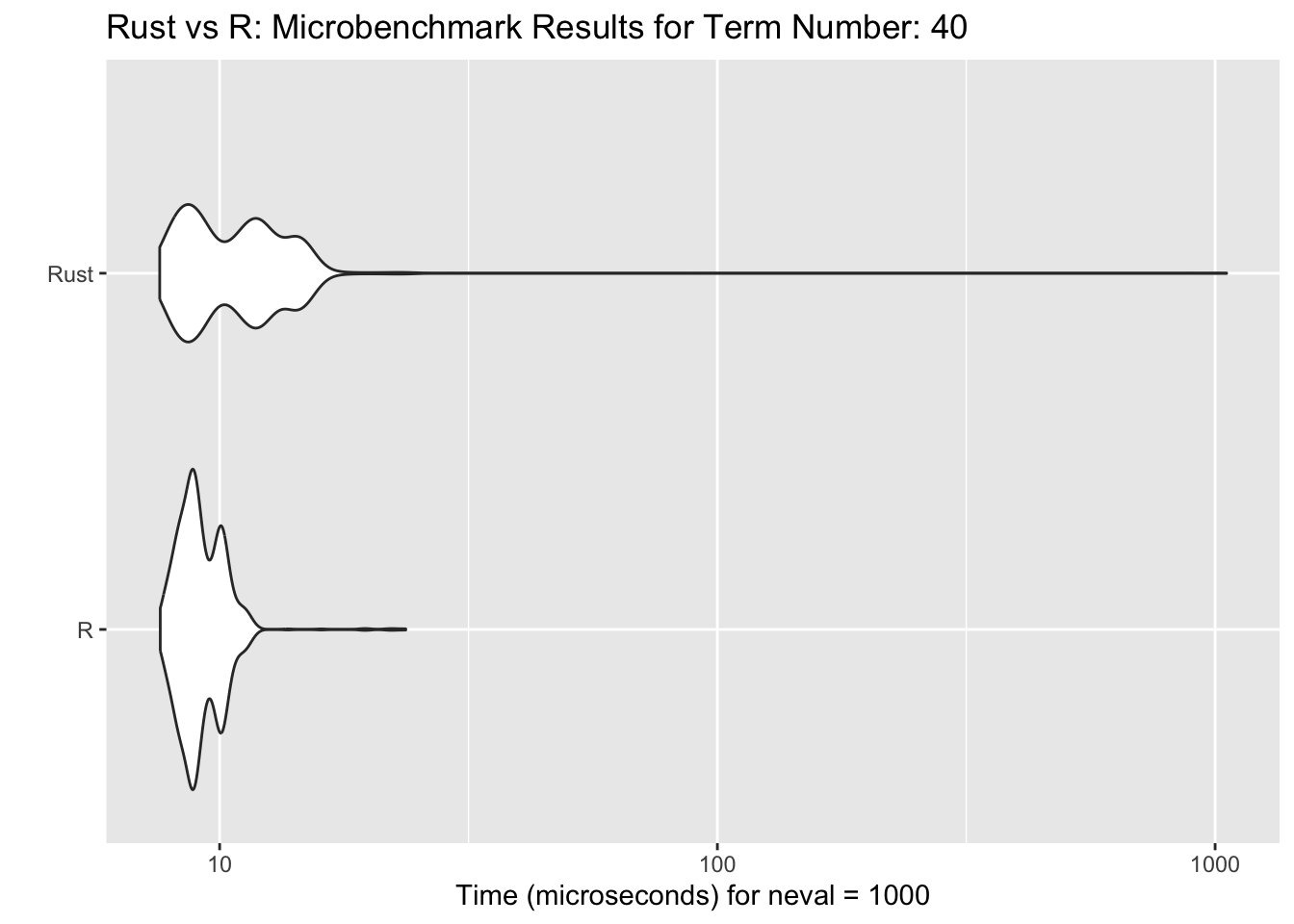
# plot benchmark times, term number = 40
autoplot(compare[[1]]) +
ggtitle(sprintf("Rust vs R: Microbenchmark Results for Term Number: %d", values[1]))
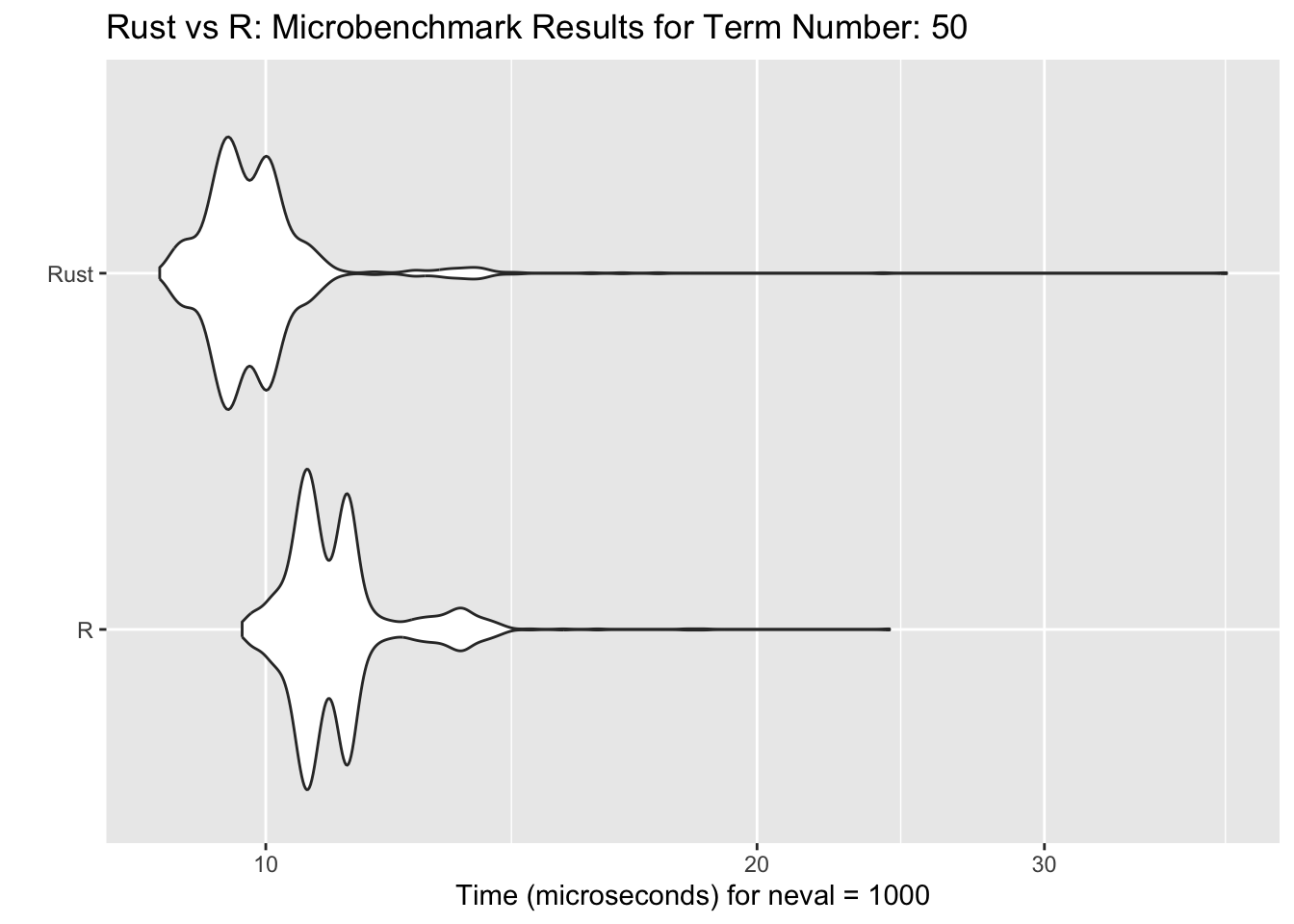
# plot benchmark times, term number = 50
autoplot(compare[[2]]) +
ggtitle(sprintf("Rust vs R: Microbenchmark Results for Term Number: %d", values[2]))
# plot benchmark times, term number = 60
autoplot(compare[[3]]) +
ggtitle(sprintf("Rust vs R: Microbenchmark Results for Term Number: %d", values[3]))
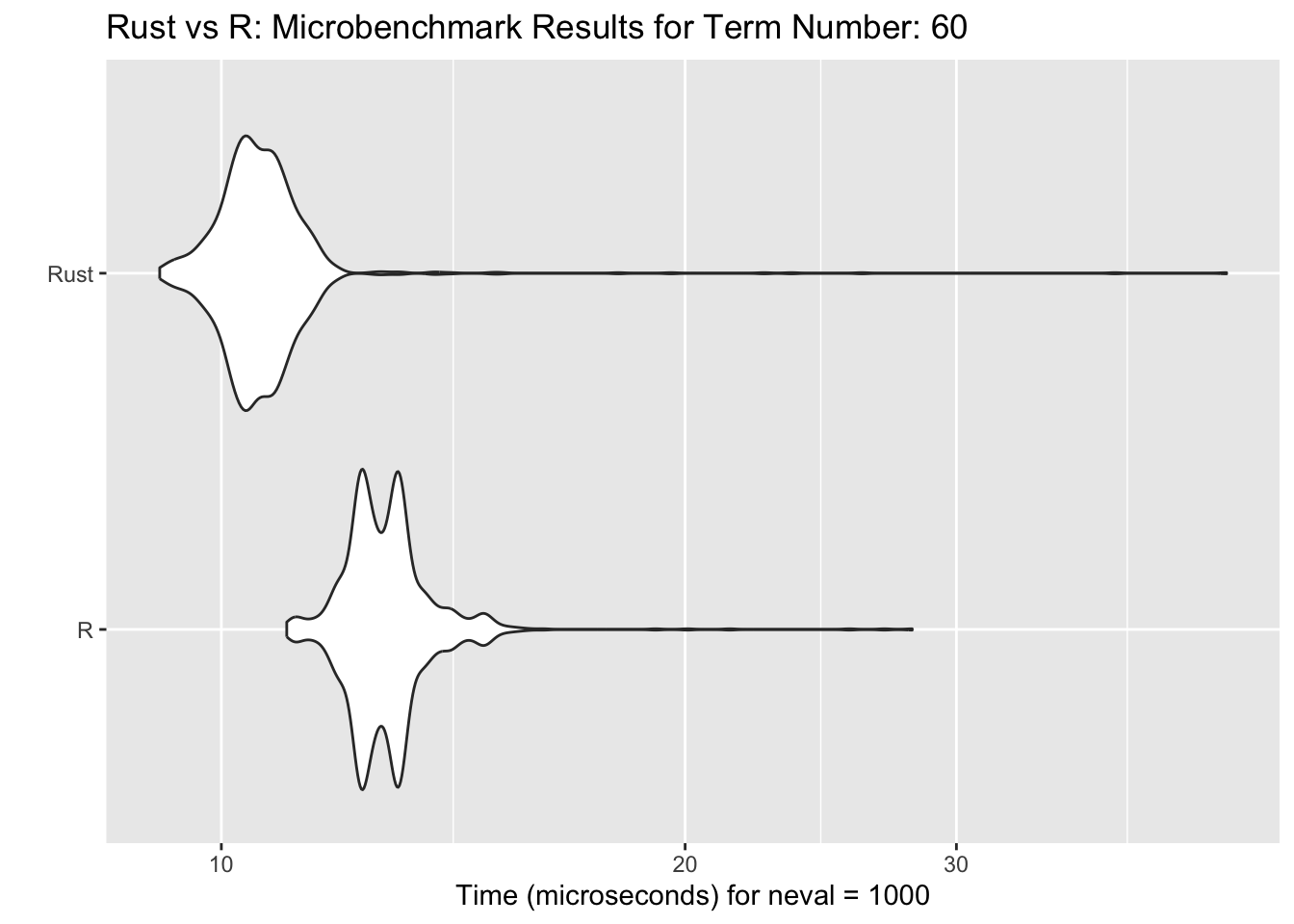
Note that while the R function appears to be faster when n=40, the Rust function tends to do better speed wise when n gets larger. That said, the Rust function appears to have instances where it runs much longer than the R function.